First off, I made a few code changes so that it would compile with my compiler, as well as I commented on a few coding changes I made.
Code: Select all
/#include "stdafx.h"
#include <iostream>
#include <windows.h>
using namespace std;
int fib (int n);
int main()
{
int n, answer;
cout << "Enter number to find: ";
cin >> n;
cout << "\n\n";
answer = fib(n);
cout << answer << " Is the " << n << "th Fibonacci number\n";
//Sleep(50000); // I added the sleep
cin >> answer; // I changed this because calling sleep is an awful habit to get into. It is very cpu intensive,
// calling cin just waits for an input thats not null then exits in this case.
return 0;
}
int fib(int n)
{
cout << "Processing fib)" << n << ")...";
if (n < 3)
{
cout << "Return 1!\n";
return(1);
}
else
{
cout << "Call fib(" << n-2 << ") and fib(" << n-1 << ").\n";
return( fib(n-2) + fib(n-1));
}
}
Note: I'm awful at explaining things.
The fib(int n) function calls itself in the return statement You can see that
The Fibonacci series is found using recursion.
Mathematically it can be shown as
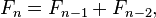
. You can see that the series is defined using Fib(n-1) + Fib(n-2), the same as your return statement.
When your return statement is called, it calls fib using n-1, without actually ever finishing the return statement. Instead it goes on to call fib(n-1), creating a sort of back order or stack of functions that have been called. These are stored on the computers stack, which you will learn about later on. It keeps on doing this until eventually the base case is reached (n < 3). Every time it calls fib(n-1) it creates a stack of function calls. You know each function is never finished until the base case is reached. One the base case is reached, fib finally returns a value of 1. Once this happens, it has a "stack" of fib calls to return through, finally able to close all those open function calls until it gets back to the very first fib(n) call where it returns a value to answer which is then printed to the screen. As you can see on every return call it calls fib twice. I don't exactly remember how it handles both calls, of whether or not it handles the fib(n-2) after all the fib(f-1) have returned or not.
If someone knows feel free to remind me.
Also, I realize my explanation may be confusing, It's a hard concept to grasp, but even harder to explain (for me personally). I suggest you do some looking up on recursion, and if you really want an understanding take a look at induction. It's a way to prove things mathematically. Hopefully someone will come along and can explain it a little bit better then I can. Let me know if anything doesn't make sense and I will try.





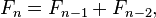 . You can see that the series is defined using Fib(n-1) + Fib(n-2), the same as your return statement.
. You can see that the series is defined using Fib(n-1) + Fib(n-2), the same as your return statement.