In addition, here are some pictures of my ugly ass at the final presentation. Marcel and Jarrod (of Dual-Threat Studios) were present. We got some pretty sweet footage as well for AiGD Chapter 18:

Explaining the separating axis theorem to a bunch of confused electrical engineers

Discussing the issues with the OBB collision kernel (addressed later in this post).

Showing off several demonstrations to the class.

[b]Rigid Body Representation[/b]

Last I posted, the engine was a complete mass-aggregate physics engine. The only thing missing was the mathematics of rotation (which just so happened to be the most complex part of the entire goddamn project). The first thing needing to be introduced was an attribute representing how easily an object tends to rotate about the z-axis. This entity is the angular analog of mass known as the moment of inertia. As with mass, the physics engine only deals with the INVERSE of the moment of inertia. This reduces floating poing divisions and allows us to represent an infinite moment of inertia in our engine as a simple floating point zero. The final rigid body attribute structure wound up being:

typedef struct _gyroStaticAttrib { 	float _inverseMass; 	float _coeffOfRestitution; 	float _damping; 	float _invMomOfInertia; 	float _angDamping; } __attribute__ ((aligned (16))) gyroStaticAttrib; 

The only other addition was the "_angDamping" attribute, which may be used to simulate friction. It's the amount of rotational velocity lost each frame. 

Along with the "attribute" structure, I also needed to add kinetic rotational attributes to our physical rigid body structure:

typedef struct _gyroRigidBody { 	gyroVector2 _velocity; 	gyroVector2 _acceleration; 	gyroVector2 _prevAccel; 	gyroVector2 _forceAccumulator; 	float _rotation; 	float _angularAccel; 	float _torqueAccum; 	unsigned int _collidableIndex; 	unsigned int _attribIndex; } __attribute__ ((aligned (16))) gyroParticle; 

"_rotation" is the angular analog of "_velocity," "_torque" is the angular analog of "_acceleration," and "_torqueAccum" is the angular analog of "_forceAccum."

[b]Rigid Body Integration/Force Application[/b]

Not a whole lot changed as far as the integration phase of the pipeline is concerned... instead of just updating linear values, the angular values are updated as well.

According to some fancy physics principle that I have forgotten, the application of a force to an object results in both a linear acceleration and an angular torque being applied to a point. With Rigid Bodies, a force may be applied to a certain point to cause rotation, as opposed to mass-aggregates, where every force is implicitly applied to the origin of the object.

[b]Velocity Contact Resolution[/b]

The two most time consuming, complex, and daunting tasks in the entire engine were the two collision resolution routines. The velocity of two colliding bodies has to be adjusted as well as their interpenetration in two separate, independent steps.

When resolving the velocities of two colliding bodies, I have chosen to use impulse-based mathematics. While these are not quite accurate in real life (nothing directly manipulates a position or its first derivative), almost every game engine uses them, because they're faster and simpler to model. Impulse-based mathematics are based around Newton's law f=ma, except that an "impulse" is applied to alter an object's velocity rather than a force (i = mv).

The first portion of the velocity resolution function calculates the total amount of inertia at the point of contact from four contributing components: Body A's linear inertia, Body A's angular inertia, Body B's linear inertia, and Body B's angular inertia. 

totalDeltaVelPerImp = _attribPool[_partPool[_colPool[_conPool[index]._colIndex[0]].partIndex]._attribIndex]._inverseMass; rotPerImp = gyroVector2ScalarCrossProd(&_conPool[index]._relContactPos[0], &_conPool[index]._normal); rotPerImp *= _attribPool[_partPool[_colPool[_conPool[index]._colIndex[0]].partIndex]._attribIndex]._invMomOfInertia; gyroVector2VectorCrossProd(&velPerImp, &_conPool[index]._relContactPos[0], rotPerImp); totalDeltaVelPerImp += gyroVector2DotProd(&velPerImp, &_conPool[index]._normal); totalDeltaVelPerImp += _attribPool[_partPool[_colPool[_conPool[index]._colIndex[1]].partIndex]._attribIndex]._inverseMass; rotPerImp = gyroVector2ScalarCrossProd(&_conPool[index]._relContactPos[1], &_conPool[index]._normal); rotPerImp *= _attribPool[_partPool[_colPool[_conPool[index]._colIndex[1]].partIndex]._attribIndex]._invMomOfInertia; gyroVector2VectorCrossProd(&velPerImp, &_conPool[index]._relContactPos[1], rotPerImp); totalDeltaVelPerImp += gyroVector2DotProd(&velPerImp, &_conPool[index]._normal); 

Next, we calculate the desired overall change in velocity between the two objects. This change is in the opposite direction (of the contact normal) with a  magnitude scaled by the coefficient of restitution. The coefficient of restitution allows us to model bodies as "extremely bouncy"--shooting apart at nearly equal speeds, or "sticky"--squashing together and continuing to move as one body.

We now know the total amount of velocity change that we desire (part 2) and the total amount of velocity change per a single unit impulse (part 1). Now we wish to find the impulse needed to give us the desired velocity change of 2. 

It's as simple as dividing our result from part 2 by our result of part 1. This gives the magnitude of our impulse. And of course, this impulse is to be applied in the direction of the contact normal:

impulseMag = _conPool[index]._deltaVelocity / totalDeltaVelPerImp; gyroVector2Scale(&impulse, &_conPool[index]._normal, impulseMag); 

Now comes the cool part. What proportion of the impulse does each body get? How much does body A rotate? How much does body B move linearly? Each impulse is scaled and applied based on the contribution of each body to the total amount of inertia involved in the contact. If Body A had a high amount of linear inertia and a low amount of angular, it will receive most of its portion of the impulse as a rotation. If Body B had a high moment of inertia and low mass, it will receive most of its impulse as a linear motion.

gyroVector2Scale(&velDelta[0], &impulse, _attribPool[_partPool[_colPool[_conPool[index]._colIndex[0]].partIndex]._attribIndex]._inverseMass); rotDelta[0] = gyroVector2ScalarCrossProd(&impulse, &_conPool[index]._relContactPos[0]); rotDelta[0] *= _attribPool[_partPool[_colPool[_conPool[index]._colIndex[0]].partIndex]._attribIndex]._invMomOfInertia; gyroVector2ScaleTo(&impulse, -1.0f); gyroVector2Scale(&velDelta[1], &impulse, _attribPool[_partPool[_colPool[_conPool[index]._colIndex[1]].partIndex]._attribIndex]._inverseMass); rotDelta[1] = gyroVector2ScalarCrossProd(&impulse, &_conPool[index]._relContactPos[1]); rotDelta[1] *= _attribPool[_partPool[_colPool[_conPool[index]._colIndex[1]].partIndex]._attribIndex]._invMomOfInertia; 

[b]Interpenetration Contact Resolution[/b]

Luckily, for the technique that I decided to go with for interpenetration resolution, the mathematics were quite similar to velocity resolution. Instead of dealing with impulses based on the total amount of velocity change, we deal with a position change based on the depth of penetration. We move/rotate each object in proportion to its total inertial contribution in the direction of the contact normal, so that they are no longer interpenetrating.

[b]GPGPU Acceleration[/b]

As you should know, the entire point of the class was that we were supposed to be hardware accelerating some CPU-bound task with either an FPGA, GPU,  or other coprocessor/microcontroller (hopefully as an optimization). I chose to use the GPU with OpenCL.

The initial setup to use OpenCL really wasn't half bad. The worst part is the fact that if you're compiling your GPU-based program at run-time, you are forced to debug compiler errors through your own in-game console/terminal window. The other worst part is that there is almost no way to debug your shit once it gets GPU side. There's no printf, cout, or way to step through your code, so you REALLY have to make damn sure it's solid before trying to migrate ANYTHING over.

You probably noticed the alignments on my data structures in the previous snippets:

__attribute__ ((aligned (16))) gyroParticle; 

This is to force both compilers (CPU and GPU-side) to allocate each struct instance to be the same size (so that arbitrary, inconsistent padding isn't used, which REALLY sucks). 

Of the entire pipeline, I managed to move everything minus collision resolution over to OpenCL as GPU-executing Kernels. That's Integration, Transformation, and Collision Detection. Unfortunately, each contact that is resolved can potentially push other contacts further into penetration, so the algorithm is iterative by nature (each contact touching a resolved contact must be updated, before another set of contacts is updated). This makes it a poor candidate for parallelism at the data-level…

The integration kernel was really straightforward. It was basically just a function with a bunch of floating-point calculations to update the state of the rigid body:

__kernel void Integrate(__global gyroParticle * partPool,  __global gyroStaticAttrib * attribPool, __global gyroCollidable * colPool, const float deltaTime, const unsigned int count) { 	int i = get_local_id(0); 	if(i > count) return; 	__global gyroParticle *part = &partPool[i ]; 	__global gyroStaticAttrib *attrib = &attribPool[i ]; 	__global gyroCollidable *col = &colPool[i ]; 	 	//Calculate linear acceleration with force input 	part->_prevAccel.x = part->_acceleration.x; 	part->_prevAccel.y = part->_acceleration.y; 	gyroVector2AddScaled(&part->_prevAccel, &part->_forceAccumulator, attrib->_inverseMass); 	 	//Calculate angular acceleration from torque input 	part->_angularAccel = part->_torqueAccum * attrib->_invMomOfInertia; 	 	//Update linear velocity from linear acceleration (and impulse?) 	gyroVector2AddScaled(&part->_velocity, &part->_prevAccel, deltaTime); 	 	//Update rotation from angular acceleration (and impulsive torque?) 	part->_rotation += part->_angularAccel * deltaTime; 	 	//Damp (impose drag) 	gyroVector2ScalarMultTo(&part->_velocity, attrib->_damping); 	part->_rotation *= attrib->_angDamping; 	 	//Update position from linear velocity 	gyroVector2AddScaled(&col->instMat.pos, &part->_velocity, deltaTime); 	 	//Update orientation from rotation 	col->instMat.zAngle += part->_rotation * deltaTime; 	 	//IMPOSE DRAG AGAIN?  	//Calculate Derived Data 	part->_forceAccumulator.x = part->_forceAccumulator.y = 0.0f; 	part->_torqueAccum = 0.0f; } 

The transformation Kernel was something that I realized would be beneficial towards the end… if the GPU is already doing a bunch of parallelized-per object calculations, it might as well be doing the object-to-world coordinate transformations. I also decided to make this kernel maintain two normalized direction vectors for the two perpendicular edges of each quad. This is so that each collision check does not have to recalculate the axes of the quads:

__kernel void Transform(__global gyroCollidable* input, const unsigned int count) {                                                        	gyroVector2 localVertex[4]; 	int i = get_local_id(0);                                    	if(i > count) return;            	localVertex[0].x = -0.5f; localVertex[0].y = -0.5f; 	localVertex[1].x = 0.5f; localVertex[1].y = -0.5f; 	localVertex[2].x = 0.5f; localVertex[2].y = 0.5f; 	localVertex[3].x = -0.5f; localVertex[3].y = 0.5f; 	gyroInstTranUpdateMat(&input[i ].instMat); 	gyroInstTranVectorListMult(input[i ].worldVertex, (__global gyroMatrix4x4 *)&input[i ], localVertex, 4); 	gyroVector2Sub(&input[i ].axes[0], &input[i ].worldVertex[1], &input[i ].worldVertex[0]); 	gyroVector2Sub(&input[i ].axes[1], &input[i ].worldVertex[3], &input[i ].worldVertex[0]); 	gyroVector2Normalize(&input[i ].axes[0]); 	gyroVector2Normalize(&input[i ].axes[1]); } 

And finally, I'm sure you guessed it, the separating axis theorem-based collision check had to be moved over to the GPU. It was by far the most complex kernel and required some serious extra work. The biggest problem was that the function has to create a list of contact objects containing each contact in the frame. If there are 512 potentially executing instances of the kernel firing in parallel, how the hell is the access to this list going to be regulated or serialized, so that they don't take a shit on each other in global memory?

I looked for some kind of built-in mutex/semaphore solution in OpenCL and was surprised to find none. What I did ultimately wind up finding was a list of atomic operations. As it turned out, I only needed a single operation to be performed atomically to fix the entire scenario:

unsigned int colIndex = atom_inc(conCount); __global gyroContact *contact = &conPool[colIndex]; 

And boom, bitches! We are able to grab an index into our contact pool and increment it for the next SAT kernel in a single operation!

[b]Performance[/b]

I am not done with optimization here by any means. I am finished enough to have completed my graduate assignment for school, but there is still plenty that could be optimized with OpenCL (including taking better advantage of their built-in vector datatypes and operations). The initial overhead of transferring these pools of data to and from the PCI-E bus each frame is relatively costly. Combine that with the fact that my particular implementation of OpenGL was working completely independently of OpenCL (they were both doing whatever they pleased with the PCI-E bus), and there is some definite room for improvement.

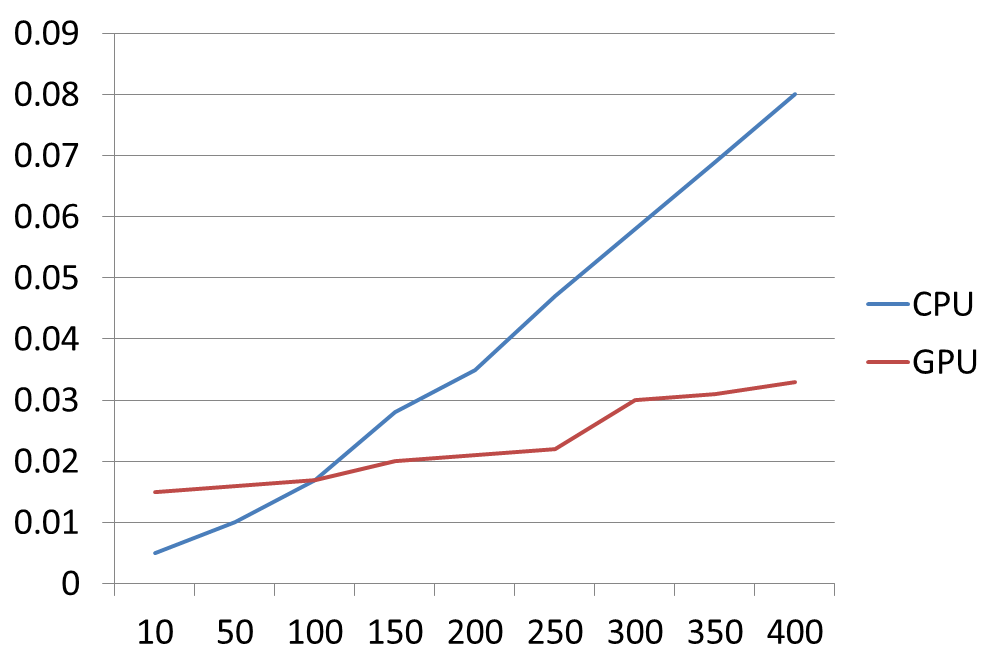
Total number of bodies simulated versus simulation time.

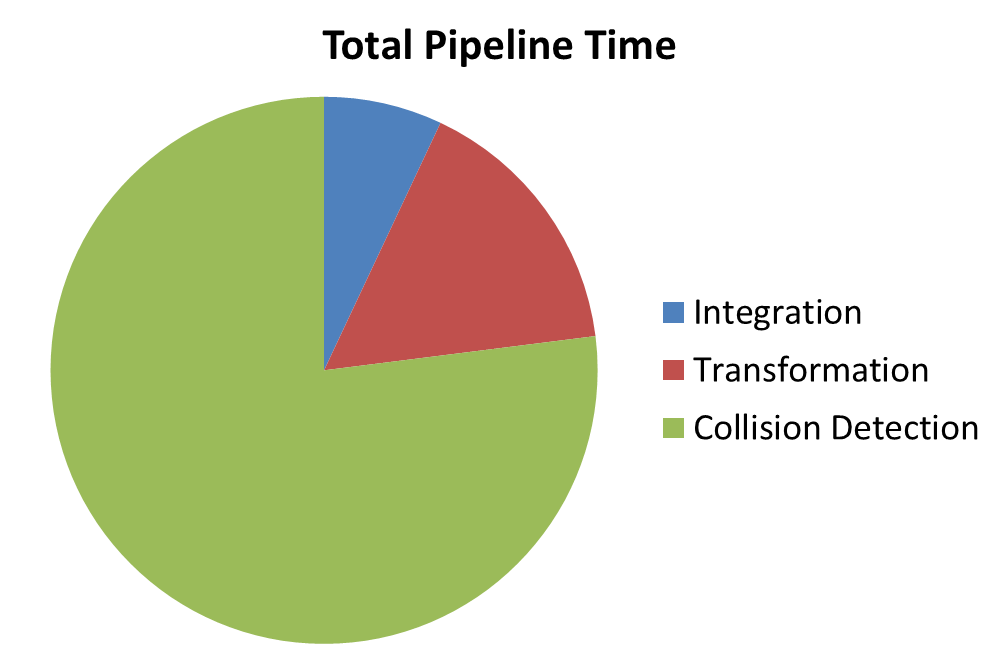
Proportion of time spent in each kernel on the GPU with 100 objects simulated.

Initially, the OpenCL implementation performs worse, because the overhead of transferring to the GPU is much greater than the overhead of physics calculations for a few objects. However, as the amount of objects on screen scale, the performance of the GPU approach begins to GREATLY increase. My Macbook can start to choke on a cock when trying to perform hundreds of OBB collision detections per frame, while the GPU can do it concurrently without blinking. When many objects were present, the physics pipeline ultimately benefited greatly from being moved to the GPU.

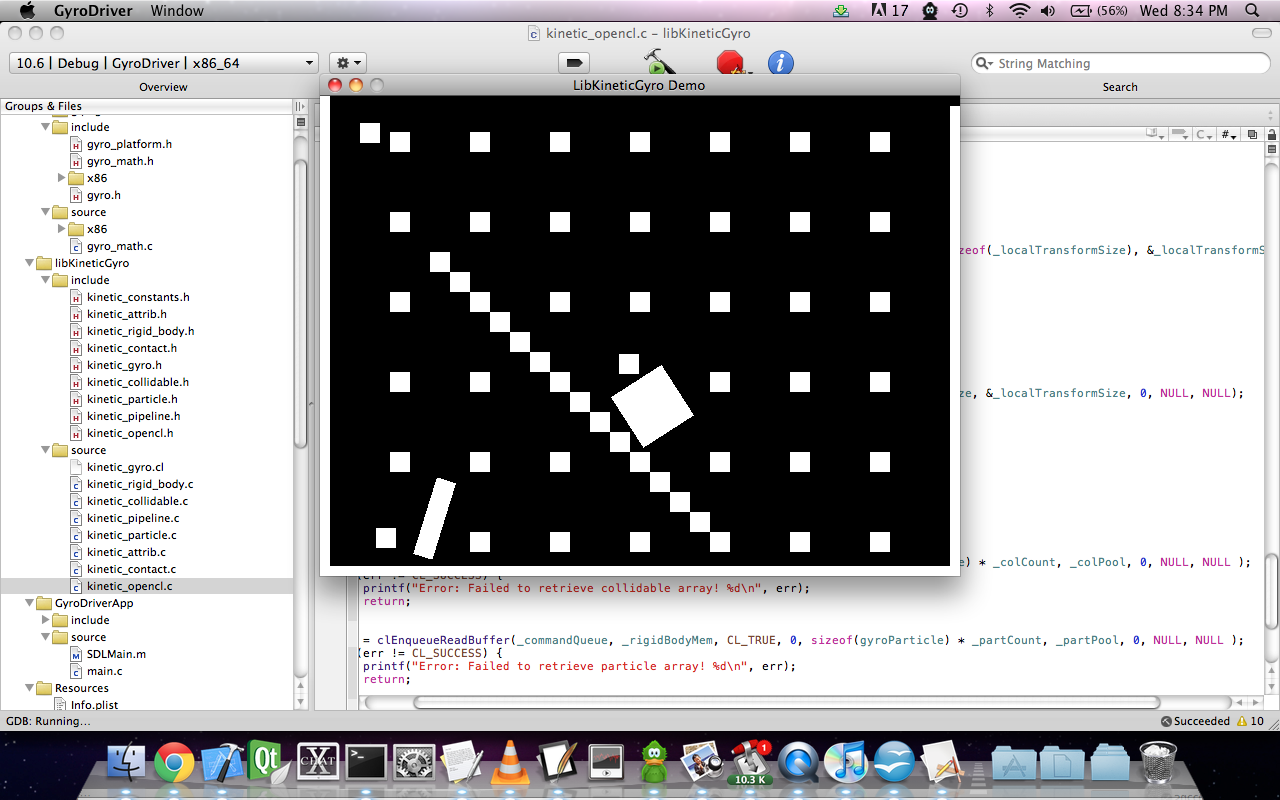
I don't really have any super cool videos/demos yet. That'll definitely be in the next dev video. I spent so much fucking time writing this post, and my final paper/presentation that I didn't really get to sit down and make a cool simulation scenario with a collapsing pyramid and shit… but just for the sake of completion heres a few screenshots with a bunch of Rigid Bodies:

First frame with gravity:

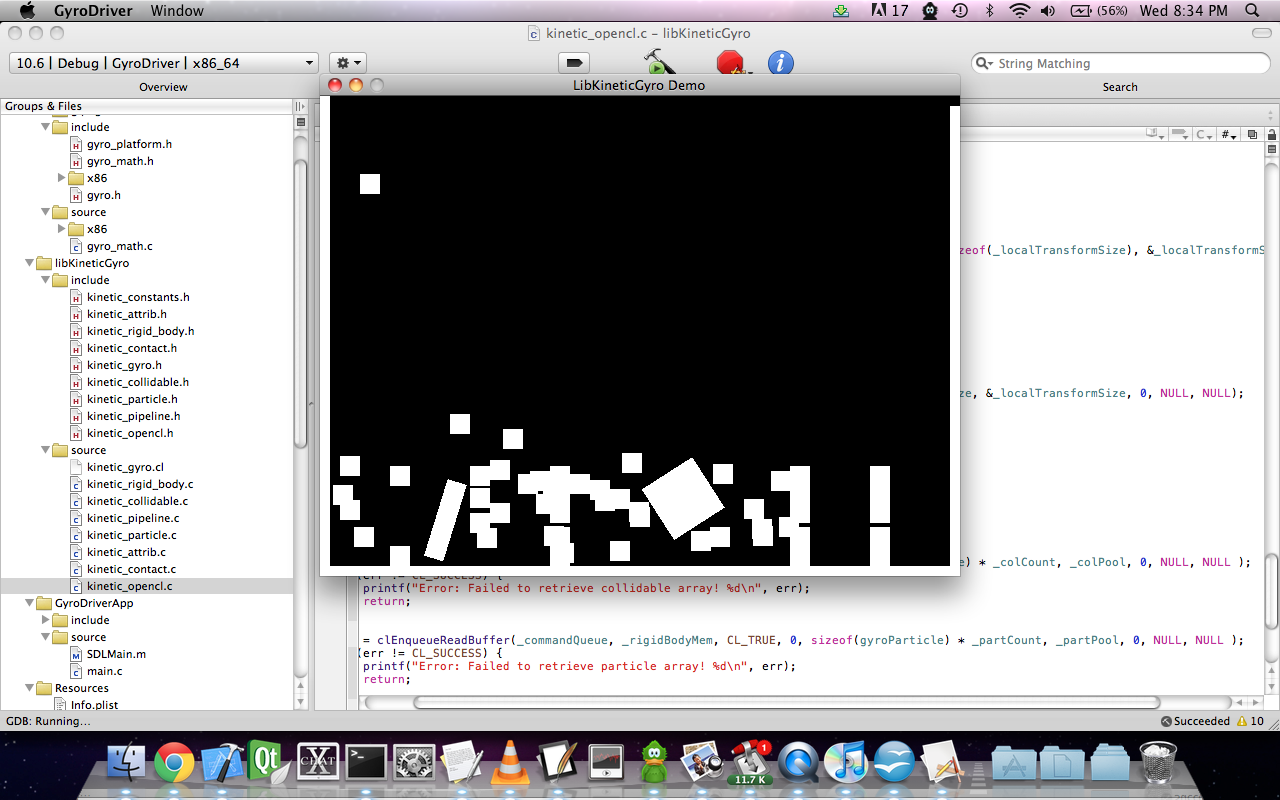
Shitloads of contacts a few frames later:

As I said before, for a shitload more info, reference my final paper and presentation here:

[url]http://elysianshadows.com/random/cpe790FINAL.pdf[/url]

[url]http://elysianshadows.com/random/CPE790FinalPresentation.pdf[/url]

[b]Future Development of LibKineticGyro[/b]

The only thing left before it's at least 100% complete is a CORRECT point of contact. I know that we had supposedly resolved this quite some time ago, but we were incorrect. It is QUITE a bitch to figure out a decent approximation for a point of contact between two quads that have already intersected… 

Another goal with this physics engine was to GRACEFULLY have support for 2D tile-based maps. Every 2D physics engine I have seen has forced 2D games to create "dynamic rigid bodies" from tiles, which must be put into a scenegraph, which are treated like any other rigid body. This significantly diminishes performance, when in reality, the physics engine can take advantage of the tile-based nature of the terrain to reduce quite a few unnecessary collision checks…

And finally, the next real step is to integrate with the Elysian Shadows engine and Toolkit. Very shortly, I would like you guys to be able to add and edit Rigid Bodies and their attributes through the Toolkit when building levels. This will add quite a bit to level development, as you'll be able to make a certain boulder unmovable until a player strong enough, build physics-based puzzles, apply forces to objects to simulate things such as wind, and many, many more applications.

Everything that I have so far has been committed to the LibKineticGyro repository (along with a very simple test driver application). The time has come… for me to not just get the fuck back to work this time. For me to get the fuck to work ON ELYSIAN SHADOWS.